Makine, satranç oynamayı nasıl bu kadar çabuk ve iyi öğrendi? Hayatımıza giren robot süpürgeler nasıl bu kadar kolay evin haritasını çıkarıp temizlik yapabiliyor? Bu soruların cevaplarını konuşacağımız blog yazım için şimdiden keyifli okumalar.
Pekiştirmeli Öğrenme Nedir?
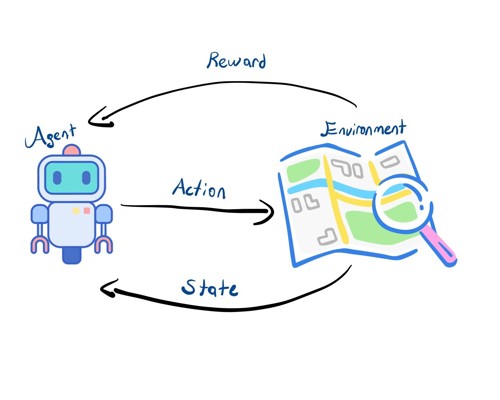
Pekiştirmeli öğrenme ödül ceza sistemine dayalı deneyimlerden öğrenme biçimidir. Pekiştirmeli öğrenmede çevre (Environment) ve bu çevrenin dinamiklerini öğrenen ajan (Agent) bulunur. Karar verici olan ajan aldığı aksiyonlar ile çevre dinamiklerine göre ödül kazanabilir veya ceza alabilir. Ajan, aldığı aksiyonlar neticesinde çevreden aldığı ödül/ceza dönütlerine bağlı olarak kazandığı ödülü maksimize edecek veya cezayı minimize edecek politikalar üretmeye çalışır. Ödülü maksimize etmek ile cezayı minimize etmek birbirinin eşleniği olan iki amaç çeşididir. Bu sebeple yazının geri kalanında ödülü maksimize etme amacını kullanacağız.
Pekiştirmeli Öğrenme Bileşenleri
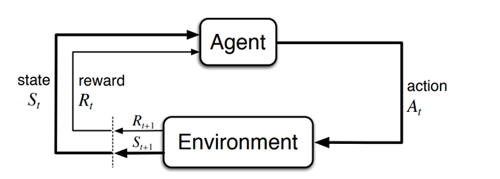
Ajanın aldığı aksiyonlar (action), mevcutta bulunduğu duruma (state) bağlı olarak farklı ödüller üretir ve ajanı farklı bir duruma geçirir. Bir başka değişle ajanın aldığı her aksiyon sonraki aksiyonlarını ve sonraki durumlarını etkilemektedir [Şekil 1]. Gerçek hayattan örnek vermek gerekirse, satranç oynarken yapılan hamleler oyunda bizi rakibimize göre farklı bir duruma getirecektir ve bu hamleler neticesinde ödül olarak rakip taşını kazanır veya ceza olarak sahip olduğumuz taşı kaybedebiliriz.
Pekiştirmeli Öğrenme İçin Doğru Amaç Fonksiyonu Nasıl Tasarlanmalı
İyi bir pekiştirmeli öğrenme için uzun vadede kazanılan ödüllerin maksimize edilmesi hedeflenir. Bu duruma satrançtan örnek vermek gerekirse oyunu kazanmak için gerekirse taş kaybı ceza maliyetine katlanılmalıdır. Peki bu amacı gerçekleyecek bir politikayı ajana nasıl öğretebiliriz? Bu sorunun cevabı konusunda Bellman Optimali Eşitliği (The Bellman Optimality Equation) bize yardımcı olmaktadır [Denklem-1].
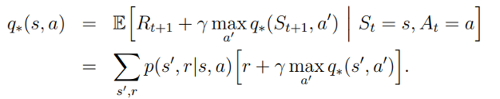
Aksiyon Sözlüğü Oluşturma
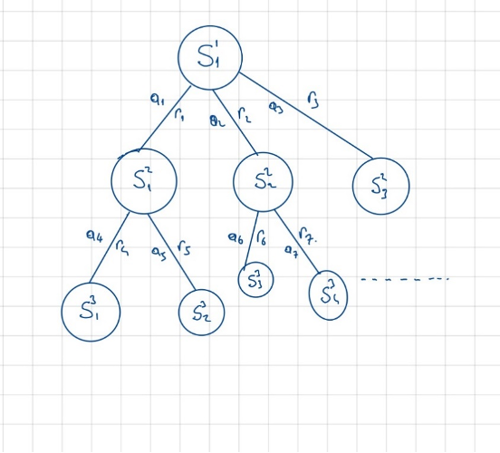
Bellman Optimali Eşitliğine (BOE) göre ajan her bir durum için ajanın aksiyon sözlüğü bulunmaktadır. Yani ajanın bulunabileceği her bir durum için ideal bir aksiyon bu listede mevcuttur(Ha Nguyen, 2021). Ajanın bulunabileceği durum sayısının çokluğu düşünüldüğünde bu sözlük oldukça kabarık bir külliyata sahip olmalıdır. Aksiyon sözlüğü oluşturulurken, içinde bulunulan durum neticesinde alınan aksiyon ve bu aksiyon neticesinde uzun vadede kazanılan ödüller dikkate alınarak ilgili duruma ait aksiyonlar ve bu aksiyonların uzun vadeli getirileri belirlenir. Her bir durum için uzun vadeli beklenen getiri hangi aksiyonda yüksek ise o aksiyon alınır. Bu durum biraz karışık gelmiş olabilir. Anlattıklarımızı aşağıdaki şekil ile netleştirelim.
Aşağıdaki şekle göre Her bir durum (s) için alınan aksiyonlar (a) neticesinde çeşitli miktarda ödül (r) kazanılıyor. Durum S11 de iken aksiyon a1 i seçtiğimizde kazandığımız kısa vadeli ödül r1 iken uzun vadeli ödül ise S21 durumunda kazanacağımız potansiyel ödüle eşittir. S21 de kazanacağımız potansiyel ödül ise bir alt basamak olan 3 basamaktaki durumlardan kazanacağımız potansiyel ödüle bağlıdır. Sonuç olarak basamağın en üstünde alacağımız kararın getirisi, kararın hemen ardından alınan ödülün yanı sıra bu kararın ajanı sürüklediği durumdan kazanılan potansiyel ödüle de bağlıdır. Tüm bu hesaplamalar göz önünde bulundurularak her bir durum için maksimum kazanılacak ödülü veren aksiyon nedir bulunur ve bu aksiyon ilgili duruma mühürlenerek durum-aksiyon sözlüğü oluşturulur. Ajan bulunduğu her durum için bu sözlüğe bakarak karar verir. Böylelikle içinde bulunduğu çevre ödülünü maksimize edecek politikaya sahip olur.
Aksiyon Sözlüğü Oluşturmanın Zorlukları
Yine satranç örneğine gelirsek 32 taş 64 karenin bulunduğu bir oyunda muhtemel durum sayısı devasa bir değere ulaşmaktadır. Devasa değere ulaşan her bir durum için hatırı sayılır bir aksiyon sayısı da mevcuttur. Bu iki durum göz önüne alındığında satranç oyunu için durum aksiyon sözlüğünü neredeyse sonsuz olarak niteleyebileceğimiz bir eleman sayısına sahip olmalıdır. Dolayısıyla bu sözlüğü hesaplayabilmek çok da mümkün görünmemektedir.
Aksiyon Sözlüğüne Alternatif Çözüm: Genelleştirme Fonksiyonları
Bu noktada mühendislik çözümü olarak genelleştirme fonksiyonları (Approximation Functions) yardıma koşmaktadır. Genelleştirme fonksiyonları X olarak adlandırabileceğimiz bağımsız değişkenleri girdi alarak, Y olarak adlandıracağımız bağımlı değişkenlere adresleyen fonksiyonlar olarak bilinir. Makine öğrenmesi algoritmalarının birçoğu genelleştirme fonksiyonu olarak pekiştirmeli öğrenme metotlarında kullanılabilir. Bu yazıda derin öğrenme ağları (Deep Neural Network) üzerinde duracağız.
Derin Q – Ağı (DeepQNetwork – DQN)
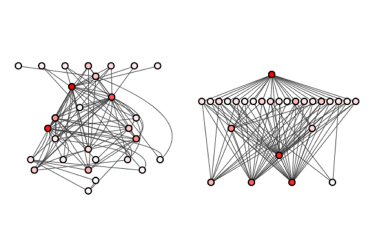
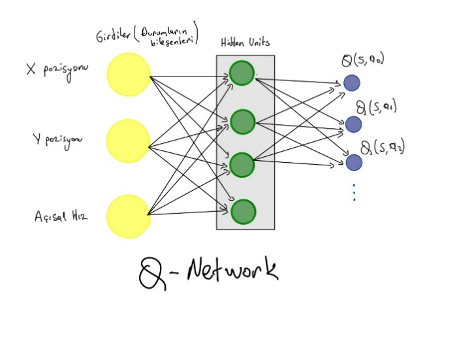
Şekil-4 de gösterildiği üzere, DQN modeli ajanın bulunduğu durumları ifade eden tüm bileşenleri girdi olarak alır. Çıktı olarak da yapabileceği her bir aksiyondan elde edebileceği toplam ödül miktarını ifade eden regresyon modeline döner. Yani girdi değişkenlerinin boyutu durumu ifade eden bileşen sayısına eşit iken, çıktı değişkeninin boyutu ise yapılabilecek aksiyon sayısına eşittir. DQN modeli her bir durum için yapılabilecek tüm aksiyonların üretebileceği aksiyon değerlerini üretmeyi hedefler ve ajan bu değerlerden hangisi maksimum ise o aksiyonu seçerek karar verir.
Ajanın çevreden topladığı her bir durum- ödül ikililerini tek tek DQN modeline koymak DQN modelinin öğrenmesi açısından güçlük teşkil eder. Çünkü pekiştirmeli öğrenmede kazanılan ödüller, aynı dağılıma sahip değildir. DQN modelleri de ezberleme (overfitting) durumuna karşı dirençsiz oldukları için ödül dağılımındaki stabil olamama durumunu karşısında öğrenme durumu oldukça zayıflar. Bu durumu çözmek için 2 mühendislik çözümünü birlikte uygulayacağız.
İlk olarak ajanın çevreden edindiği her bir geri dönüşü direkt olarak öğrenme yerine bu geri dönüşleri biriktirip gruplar halinde (batch) modele koyacağız. Bu grubun elaman sayısı sabit olacak fakat çevreden geri dönüş geldikçe gruba belirli sayıda örneği ekleyip aynı sayıda örneği de çıkararak gruptaki bilgi sirkülasyonunun olmasını sağlayacağız.
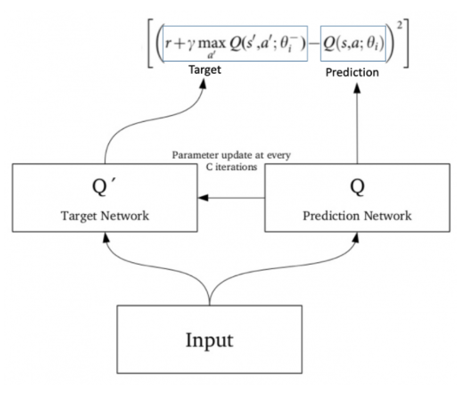
İkinci olarak tek bir network modeli yerine tahmin ve hedef olmak üzere 2 model kullanacağız. Tahmin modeli her bir iterasyonda öğrenen bir network iken hedef modeli ise belirli bir iterasyon periyodu sonunda tahmin modeline eşitlenerek elde edilen networktur. Bu yöntem ile hedef değişkendeki stabil olamama durumunun hafifletilmiş olunması amaçlanmaktadır [Şekil-5].
Uygulama: Sarkaç oyunu

Sarkaç oyununda bir ucu menteşeye sabitlenmiş çubuk sağa ve sola tork uygulanarak dik konuma getirilmesi amaçlanmaktadır. Uygulanabilecek tork’un büyüklüğü -2 ile 2 arasında değişebilmektedir. Oyunun her bir episode ’unda 200 kez aksiyon yapılabilmektedir ve 200 aksiyon sonunda ilgili episode bitmektedir.
Durum Bileşenleri
Sarkacın bulunduğu durum 3 bileşen ile gösterilmektedir. Bu bileşenlerin ayrıntıları tablo-1 tabloda gösterilmektedir.

Ödül
Sarakça uygulanabilecek her aksiyon sonrasında elde edilebilecek ödül miktarı denklem 2’de gösterildiği gibi formülize edilebilir.
theta: Sarkacın [-pi, pi] arasında normalize edilmiş açısıdır. Sarkaç dik konumundayken 0 değerini alır. Bu eşitliğe göre kazanılabilecek minimum ödül miktarı: –16.2736044 iken maksimum ödül miktarı da 0’dır.Sarkaç maksimum ödül miktarını yukarı yönlü dik ve uygulanan tork değeri 0 iken alır. Dolayısıyla sarkacı dik pozisyona getirme amacına uygun bir ödül değeri vardır.
Modelleme
DQN modelini sarkaç oyununa uygulayalım. DQN modeli temelde belirli sayıda aksiyon listesi için oluşturulmuştur. Fakat sarkaç oyununda alınabilecek aksiyonlar [-2,2] arasında sonsuz değere sahiptir. Bu noktada bir mühendislik çözümü olarak -2 ile 2 arasında 11 adet eşit aralıklı sayı grubu oluşturarak sarkacın sonsuz sayıda olan aksiyon listesini 11’e indirgeyebiliriz. Böylelikle sarkacın aksiyon yelpazesini daraltmış olsak da DQN modelini uygulayabilir noktaya gelmiş bulunuyoruz. DQN modeli için tasarlanan öğrenme ortamının bilgileri aşağıdaki gibidir.
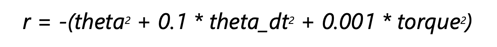
[-2,-1.6,-1.2,-0.8,-0.4, 0, 0.4, 1.2, 1.6, 2]
-500 adet episode koşulmuştur.
-İlk episodelarda ajanın farklı deneyimler deneme iştahı yüksek iken sonraki her bir episode ’da bu iştah bir önceki episode göre %97 azalacak şekilde dizayn edilmiştir.
-Yer çekimi ivmesi 9.81 alınmıştır.
-Sonraki hareketlerden kazanılabilecek potansiyel ödüllerin ağırlıkları (GAMMA değeri) 0,98 olarak alınmıştır.
-Hedef ve tahmin olmak üzere iki DQN modeli inşa edilmiştir. Bu modeller ilk başta birbirine denk yapı taşlara sahiptir.
-Eğitim için biriktirilen hafıza topluluğu sayısı (memory size) 100.000 adettir. Bu hafıza topluluğa eklenip/çıkarılacak örneklem (min experience) sayısı 100 adettir.
Derin Q-Ağı modelinin sözde kodu Şekil 5’teki gibi ifade edilmiştir.

Modelin eğitilmesi oldukça uzun sürebilmektedir. Ben kendi bilgisayarımla modeli eğitmek için yaklaşık 1 günümü harcadım. Eğitilen model sonucunda oyunu ajana oynattığımızda aşağıdaki gibi oynamaktadır.

Oyunu yeterince öğrenmiş görünüyor. Hatta en yükseğe çıkmak için geri gelip gerilmeyi de ihmal etmiyor. 😊
Modelin bu manevra kabiliyetini öğrendiğini izlemek oldukça keyifli. 😊
Ajana oyunu öğretirken içinde bulunulan durumun modele girdi teşkil edilebilecek sayısal değerler ile ifade edilmesi gerekmektedir. Sarkaç oyunu için, ajanın içinde bulunduğu durum konum ve hız bileşenleri ile sayısal değerlere dönüştürülmüştü. Bu noktada bazı problemlerin çözümü için işimiz daha da karmaşık olabilir. Örneğin atari oyunları ele alınırsa ajanın içinde bulunduğu durumun resmi çekilip görüntü işleme teknikleri ile ajanın içinde bulunduğu durum sayısallaştırılabilir(Li et al., 2020). Görüntü işleme teknikleri ile pekiştirmeli öğrenme çözümü bir başka blog yazımın konusu olabilir.
Kaynakça
-Ha Nguyen. (2021, March). Plating Mountain Car with Deep Q-Learning.
-Li, Y., Fang, Y., & Akhtar, Z. (2020). Accelerating deep reinforcement learning model for game strategy. Neurocomputing, 408, 157–168. https://doi.org/10.1016/j.neucom.2019.06.110
-Sutton, R. S., & Barto, A. G. (2014). Reinforcement Learning: An Introduction Second edition, in progress.
-Ulukuş, M. Y. (2023). (2023) BVA529E: [Reinforce.Lear.for Busi.App.], [Bahar Dönemi]. [İstanbul Teknik Üniversitesi].







 Önceki
Önceki